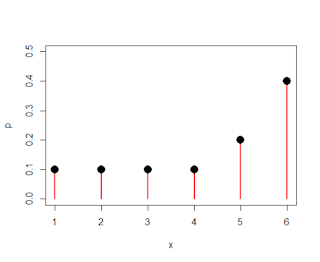
 |
| Discrete population, with different probabilities associated with different numbers |
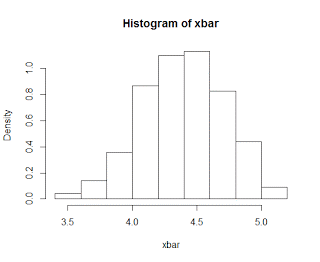 | ||||
| Sampling distribution of means from the discrete parent population, with a sample size of n=30 |
In the last post, we left the central limit theorem defined as a normally-distributed sampling distribution of means reflecting the shape of the normally-distributed parent population, but with a smaller spread and less variance. However, what happens when we sample from a non-normal distribution, such as an exponential distribution or a discrete distribution?
As it turns out, the sampling distribution of means is also normal, regardless of the shape of the parent population. This holds for sample sizes of about 30 or more, which is why the central limit theorem is also sometimes referred to as the law of large numbers.
This is shown in the following video, and can be modified with this R script.
