I thought I'd blog outside today, to create a more informal setting. I was hoping we could talk a bit; you know, rap.
This week I taught my class about main effects and interactions - namely, how to eyeball a graph and determine whether there is a main effect, an interaction, or both. For those new to statistics or graphing results, there are a couple of mnemonics you can use to make an educated guess about which factors have a main effect, and if there is an interaction, what is driving it.
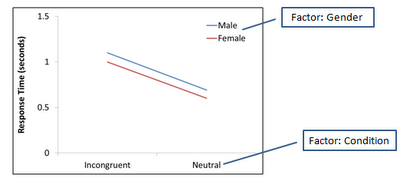
Example: Let's say we have a 2x2 factorial design. One factor is Gender with two levels: Male and Female. The other factor is Condition, also with two levels: Incongruent and Neutral. Gender is a between-subjects factor, since it is based on a population characteristic that is fixed (such as gender or handedness), while Condition is a within-subjects factor, since each participant is exposed to each level of that factor. We test them on a classic Stroop paradigm where they respond to the color of the word, not the word itself. We gather some data, average the reaction times for each combination of levels, and obtain the following results:
In this case, there is no main effect of Gender; on average, Males and Females have the same reaction times. (Remember to look at the averages of the endpoints of the lines.) There does appear to be a main effect of condition, as the middle of the colored lines are different from each other. However, there is an interaction as well, as reaction time is dependent upon both the level of Gender and the level of Condition. In other words, if someone asked you whether Males had different reaction times than Females for a stroop task, you would say that it depends on which condition they are in.
This same rationale can be applied to main effects and interactions for beta weights extracted from FMRI data; simply replace reaction time with beta weights for the dependent variable, and the interpretations are the same.
This week I taught my class about main effects and interactions - namely, how to eyeball a graph and determine whether there is a main effect, an interaction, or both. For those new to statistics or graphing results, there are a couple of mnemonics you can use to make an educated guess about which factors have a main effect, and if there is an interaction, what is driving it.
Example: Let's say we have a 2x2 factorial design. One factor is Gender with two levels: Male and Female. The other factor is Condition, also with two levels: Incongruent and Neutral. Gender is a between-subjects factor, since it is based on a population characteristic that is fixed (such as gender or handedness), while Condition is a within-subjects factor, since each participant is exposed to each level of that factor. We test them on a classic Stroop paradigm where they respond to the color of the word, not the word itself. We gather some data, average the reaction times for each combination of levels, and obtain the following results:
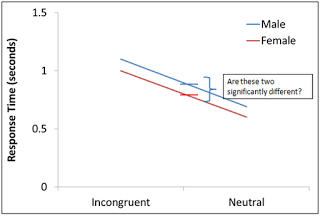
Overall, we can see that Females are faster, on average, than males - regardless of which condition they are in. In other words, there appears to be a main effect of Gender. (Note that in these examples no mention is given to standard error; however, for the moment, assume that the standard error is zero.) Another way to look at this is to determine whether the middle of the colored lines are significantly different from each other:
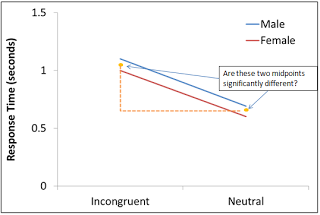
Likewise, can we ask whether there is a main effect of condition by looking at the average for the Incongruent condition, collapsed across levels of both Male and Female, to the average of the Neutral condition, collapsed across levels of both Male and Female. ("Collapsed" here simply means "Averaged"; in other words, what was the reaction time across all subjects for the Incongruent condition and the Neutral condition?) To look visualize this main effect in the graph, we can compare the averages of the endpoints of each line:
Now, let's ask whether there is an interaction: In other words, does reaction time depend on both the level of Condition and the level of Gender? In this case, the answer would be no; females are faster than males, regardless of which condition they are in. So if it doesn't depend on which condition they are in, there is no interaction.
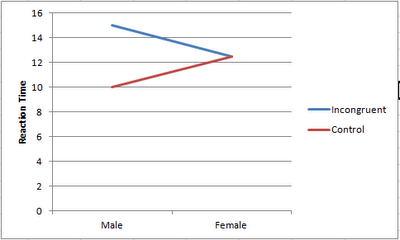
What does an interaction look like? Usually if the lines are crossed (or tending towards a crossing of each other) you can say that there is likely an interaction. (The calculation of an interaction is slightly more complicated than this, but for most purposes this assumption holds.) For example, let's modify the reaction times a bit and say that Females had the same reaction time regardless of which condition they were in, while Males were slower than Females in the Incongruent condition but faster in the Control condition:
This same rationale can be applied to main effects and interactions for beta weights extracted from FMRI data; simply replace reaction time with beta weights for the dependent variable, and the interpretations are the same.