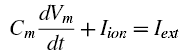Computational modeling can be a tough nut to crack. I'm not just talking pistachio-shell dense; I'm talking walnut-shell dense. I'm talking a nut so tough that not even a nutcracker who's cracked nearly every damn nut on the planet could crack this mother, even if this nutcracker is so badass that he wears a leather jacket, and that leather jacket owns a leather jacket, and that leather jacket smokes meth.
That being said, the best approach to eat this whale is with small bites. That way, you can digest the blubber over a period of several weeks before you reach the waxy, delicious ambergris and eventually the meaty whale guts of computational modeling and feel your consciousness expand a thousandfold. And the best way to begin is with a single neuron.
The Hodgkin-Huxley Model, and the Hunt for the Giant Squid
Way back in the 1950s - all the way back in the twentieth century - a team of notorious outlaws named Hodgkin and Huxley became obsessed and tormented by fevered dreams and hallucinations of the Giant Squid Neuron. (The neurons of a giant squid are, compared to every other creature on the planet, giant. That is why it is called the giant squid. Pay attention.)
After a series of appeals to Holy Roman Emperor Charles V and Pope Stephen II, Hodgkin and Huxley finally secured a commission to hunt the elusive giant squid and sailed to the middle of the Pacific Ocean in a skiff made out of the bones and fingernails and flayed skins of their enemies. Finally spotting the vast abhorrence of the giant squid, Hodgkin and Huxley gave chase over the fiercest seas and most violent winds of the Pacific, and after a tense, exhausting three-day hunt, finally cornered the giant squid in the darkest netherregions of the Marianas Trench. The giant squid sued for mercy, citing precedents and torts of bygone eras, quoting Blackstone and Coke, Anaxamander and Thales. But Huxley, his eyes shining with the cold light of purest hate, smashed his fist through the forehead of the dread beast which erupted in a bloody Vesuvius of brains and bits of bone both sphenoidal and ethmoidal intermixed and Hodgkin screamed and vomited simultaneously. And there stood Huxley triumphant, withdrawing his hand oversized with coagulate gore and clutching the prized Giant Squid Neuron. Hodgkin looked at him.
"Huxley, m'boy, that was cold-blooded!" he ejaculated.
"Yea, oy'm one mean cat, ain't I, guv?" said Huxley.
"'Dis here Pope Stephen II wanted this bloke alive, you twit!"
"Oy, not m'fault, guv," said Huxley, his grim smile twisting into a wicked sneer. "Things got outta hand."
Scene II
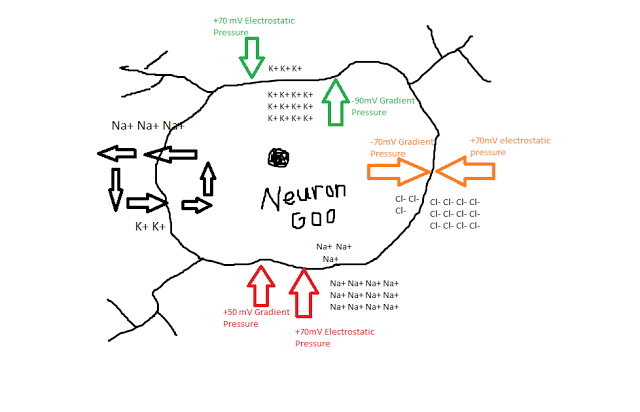
Drunk with victory, Hodgkin and Huxley took the Giant Squid Neuron back to their magical laboratory in the Ice Cream Forest and started sticking a bunch of wires and electrodes in it. To their surprise, there was a difference in voltage between the inside of the neuron and the bath surrounding it, suggesting that there were different quantities of electrical charge on both sides of the cell membrane. In fact, at a resting state the neuron appeared to stabilize around -70mV, suggesting that there was more of a negative electrical charge inside the membrane than outside.
Keep in mind that when our friends Hodgkin and Huxley began their quest, nobody knew exactly how the membrane of a neuron worked. Scientists had observed action potentials and understood that electrical forces were involved somehow, but until the experiments of the 1940s and '50s the exact mechanisms were still unknown. However, through a series of carefully controlled studies, the experimenters were able to measure how both current and voltage interacted in their model neuron. It turned out that three ions - sodium (Na+), potassium (K+), and chlorine (Cl-) - appeared to play the most important role in depolarizing the cell membrane and generating an action potential. Different concentrations of the ions, along with the negative charge inside the membrane, led to different pressures exerted on each of the ions.
For example, K+ was found to be much more concentrated inside of the neuron than outside, leading to a concentration gradient exerting pressure for the K+ ions to exit the cell; at the same time, however, the attractive negative force inside the membrane exerting a countering electrostatic pressure, as positively charged potassium ions would be drawn toward the inside of the cell. Similar characteristics of the sodium and chlorine ions were observed as well, as shown in the following figure:
In addition to these passive forces, Hodgkin and Huxley also observed an active, energy-consuming force in maintaining the resting potential - a mechanism which exchanged potassium for sodium ions, by kicking out roughly three sodium ions for each potassium ion. Even with this pump though, there is still a whopping 120mV of pressure for sodium ions to enter. What prevents them from rushing in there and trashing the place?
Hodgkin and Huxley hypothesized that certain channels in the neuron membrane were selectively permeable, meaning that only specific ions could pass through them. Furthermore, channels could be either open or closed; for example, there may be sodium channels dotting the membrane, but at a resting potential they are usually closed. In addition, Hodgkin and Huxley thought that within these channels were gates that regulated whether the channel was open or closed, and that these gates could be in either permissive or non-permissive states. The probability of a gate being in either state was dependent on the voltage difference between the inside and the outside of the membrane.
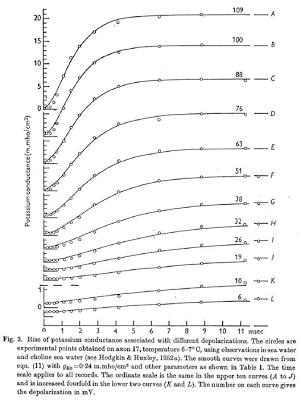
Although this all may seem conceptually straightforward, keep in mind that Hodgkin and Huxley were among the first to combine all of these properties into one unified model - something which could account for the conductances, voltage, and current, as well as how all of this affected the gates within each ion channel - and they were basically doing it from scratch. Also keep in mind that these crazy mofos didn't have stuff like Matlab or R to help them out; they did this the old-fashioned way, by changing one thing at a time and measuring that shit by hand. Insane. (Also think about how, in the good old days, people like Carthaginians and Romans and Greeks would march across entire continents for months, years sometimes, just to slaughter each other. Continents! These days, my idea of a taxing cardiovascular workout is operating a stapler.) To show how they did this for quantifying the relationship between voltage and conductance in potassium, for example, they simply applied a bunch of different currents, saw how it changed over time, and attempted to fit a mathematical function to it, which happens to fit quite nicely when you include n-gates and a fourth-power polynomial.
After a series of painstaking experiments and measurements, Hodgkin and Huxley calculated values for the conductances and equilibrium voltages for different ions. Quite a feat, when you couple that with the fact that they hunted down and killed their very own Giant Squid and then ripped a neuron out of its brain. Incredible. That is the very definition of alpha male behavior, and it's something I want all of my readers to emulate.
 |
| Table 3 from Hodgkin & Huxley (1952) showing empirical values for voltages and conductances, as well as the capacitance of the membrane. |
The same procedure was used for the n, m, and h gates, which were also found to be functions of the membrane voltage. Once these were calculated, then the conductances and voltage potential could be found for any resting potential and any amount of injected current.
 |
| H & H's formulas for the n, m, and h gates as a function of voltage. |
But stay focused here. Most of the formulas and constants can simply be transcribed from their papers into a Matlab script, but we also need to think about the final output that we want, and how we are going to plot it. Note that the original Hodgkin and Huxley paper uses a differential formula for voltage to tie together the capacitance and conductance of the membrance, e.g.:
We can use a method like Euler first-order approximation to plot the voltages, in which each time step is based off of the previous one which is added to a function multiplied by a time step; in the sample code below, the time step can be extremely small, thus giving a better approximation to the true shape of the voltage timecourse. (See the "calculate the derivatives" section below.)
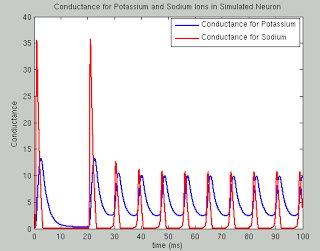
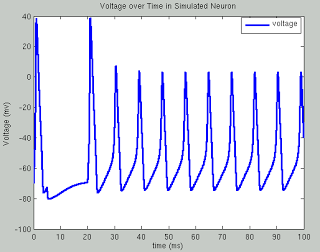
The following code runs a simulation of the Hodgkin Huxley model over 100 milliseconds with 50mA of current, although you are encouraged to try your own and see what happens. The sample plots below show the results of a typical simulation; namely, that the voltage depolarizes after receiving a large enough current and briefly becomes positive before returning to its previous resting potential. The conductances of sodium and potassium show that the sodium channels are quickly opened and quickly closed, while the potassium channels take relatively longer to open and longer to close.The point of the script is to show how equations from papers can be transcribed into code and then run to simulate what neural activity should look like under certain conditions. This can then be expanded into more complex areas such as memory, cognition, and learning.
The actual neuron, of course, is nowhere to be seen; and thank God for that, else we would run out of Giant Squids before you could say Jack Robinson.
Resources
Book of GENESIS, Chapter 4
Original Hodgkin & Huxley paper
%===simulation time===
simulationTime = 100; %in milliseconds
deltaT=.01;
t=0:deltaT:simulationTime;
%===specify the external current I===
changeTimes = [0]; %in milliseconds
currentLevels = [50]; %Change this to see effect of different currents on voltage (Suggested values: 3, 20, 50, 1000)
%Set externally applied current across time
%Here, first 500 timesteps are at current of 50, next 1500 timesteps at
%current of zero (resets resting potential of neuron), and the rest of
%timesteps are at constant current
I(1:500) = currentLevels; I(501:2000) = 0; I(2001:numel(t)) = currentLevels;
%Comment out the above line and uncomment the line below for constant current, and observe effects on voltage timecourse
%I(1:numel(t)) = currentLevels;
%===constant parameters===%
%All of these can be found in Table 3
gbar_K=36; gbar_Na=120; g_L=.3;
E_K = -12; E_Na=115; E_L=10.6;
C=1;
%===set the initial states===%
V=0; %Baseline voltage
alpha_n = .01 * ( (10-V) / (exp((10-V)/10)-1) ); %Equation 12
beta_n = .125*exp(-V/80); %Equation 13
alpha_m = .1*( (25-V) / (exp((25-V)/10)-1) ); %Equation 20
beta_m = 4*exp(-V/18); %Equation 21
alpha_h = .07*exp(-V/20); %Equation 23
beta_h = 1/(exp((30-V)/10)+1); %Equation 24
n(1) = alpha_n/(alpha_n+beta_n); %Equation 9
m(1) = alpha_m/(alpha_m+beta_m); %Equation 18
h(1) = alpha_h/(alpha_h+beta_h); %Equation 18
for i=1:numel(t)-1 %Compute coefficients, currents, and derivates at each time step
%---calculate the coefficients---%
%Equations here are same as above, just calculating at each time step
alpha_n(i) = .01 * ( (10-V(i)) / (exp((10-V(i))/10)-1) );
beta_n(i) = .125*exp(-V(i)/80);
alpha_m(i) = .1*( (25-V(i)) / (exp((25-V(i))/10)-1) );
beta_m(i) = 4*exp(-V(i)/18);
alpha_h(i) = .07*exp(-V(i)/20);
beta_h(i) = 1/(exp((30-V(i))/10)+1);
%---calculate the currents---%
I_Na = (m(i)^3) * gbar_Na * h(i) * (V(i)-E_Na); %Equations 3 and 14
I_K = (n(i)^4) * gbar_K * (V(i)-E_K); %Equations 4 and 6
I_L = g_L *(V(i)-E_L); %Equation 5
I_ion = I(i) - I_K - I_Na - I_L;
%---calculate the derivatives using Euler first order approximation---%
V(i+1) = V(i) + deltaT*I_ion/C;
n(i+1) = n(i) + deltaT*(alpha_n(i) *(1-n(i)) - beta_n(i) * n(i)); %Equation 7
m(i+1) = m(i) + deltaT*(alpha_m(i) *(1-m(i)) - beta_m(i) * m(i)); %Equation 15
h(i+1) = h(i) + deltaT*(alpha_h(i) *(1-h(i)) - beta_h(i) * h(i)); %Equation 16
end
V = V-70; %Set resting potential to -70mv
%===plot Voltage===%
plot(t,V,'LineWidth',3)
hold on
legend({'voltage'})
ylabel('Voltage (mv)')
xlabel('time (ms)')
title('Voltage over Time in Simulated Neuron')
%===plot Conductance===%
figure
p1 = plot(t,gbar_K*n.^4,'LineWidth',2);
hold on
p2 = plot(t,gbar_Na*(m.^3).*h,'r','LineWidth',2);
legend([p1, p2], 'Conductance for Potassium', 'Conductance for Sodium')
ylabel('Conductance')
xlabel('time (ms)')
title('Conductance for Potassium and Sodium Ions in Simulated Neuron')