The Will to Persevere, Induced by Deep Brain Stimulation

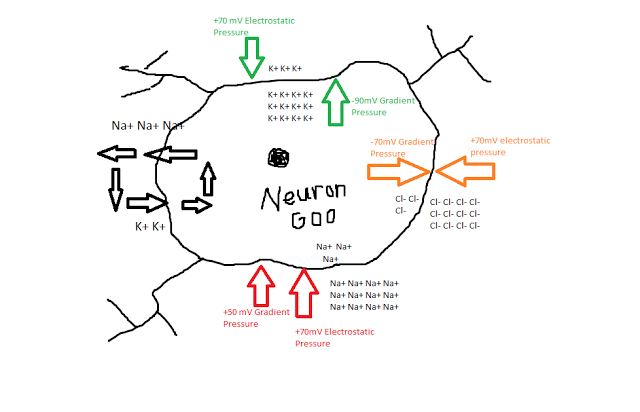
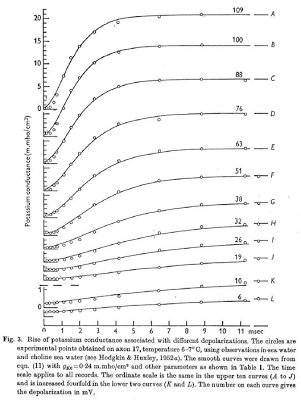
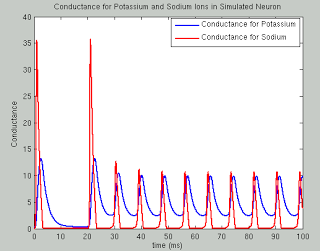
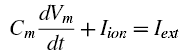Scientists, and neuroscientists in particular, are an odd bunch, with complex, multifaceted personalities. on the one hand they can be reclusive, socially awkward, and pretentious; but, in their defense, they make an honest effort to try and make up for these defects by being completely nuts.

For example, although most neuroscientists won't admit it, deep down, in their heart of hearts, somewhere in the left atrium, each and every one of feels a little twinge of excitement at the prospect of sticking electrodes somewhere in a person's brain and delivering electrical shocks. Seriously. Just ask any self-described neuroscience researcher what he would love to do most, and nine times out of ten he will say "Stick things inside someone's brain and inject enough electricity into it to light up a small amusement park." Only rarely will he give a more reasoned, more mature answer, such as "Purchase a motorcycle," or "Become an adult film star."

In any case, neuroscientists are usually prevented from acting out their sick fantasies by institutional review boards, or IRBs, which, from a neuroscientist's point of view, exist solely to be squeamish buzzkills and to put your experiments under review for a length of time equivalent to the gestation period of a yak. However, every once in a while there will be a case where an epileptic patient is undergoing a craniotomy, for example, or where a fellow neuroscientist is receiving extensive brain surgery after his latest motorcycle accident; and these cases, in addition to being like the Irish Sweepstakes for neuroscientists, can also yield valuable insights about how direct stimulation of cortical and subcortical areas can induce different physiological and cognitive states.

A recent example of this type of research appeared in a paper in the journal Neuron a couple of months ago, by Parvizi et al. Two epilepsy patients had deep-brain electrodes implanted in their brain, and the researchers were particularly interested in those electrodes located within the midcingulate region of the anterior cingulate cortex (ACC). After delivering small bursts of electricity to these electrodes, the patients reported higher levels of autonomic system activity, including increased heart rate and alertness, along with a feeling of foreboding but a concomitant feeling of resolve to overcome the intangible "challenge" that they felt. A follow-up resting-state analysis showed that both of these seed stimulation regions were hubs of a widespread cingulo-opercular network, similar to the typical coactivation of cingulate and insula responses observed in most studies examining the medial prefrontal cortex, and also involved in detecting emotional salience and sustaining goal-directed activity.

Figure 1 from Parvizi et al, showing the stimulation site in the midcingulate region for both patients, as well as more remote stimulation sites for comparison.

Figure 2 from Parvizi et al depicting a resting-state functional connectivity analysis using the midcingulate as a seed region.

The authors labeled these feelings of wanting to overcome a formidable challenge as the "will to persevere," a phrase I think will be variously interpreted, but which seems apt enough for the current paper. However, one concern that popped into my head while reading through the article (dons reviewer glasses, purses lips disapprovingly) was: Is it really a will to persevere, or just a general increase in autonomic nervous system arousal (i.e., the sympathetic branch)? The "will to persevere" reported here may be the patient's interpretation of his increased heart rate, which, given the circumstances of the experiment and the patient's undergoing surgery to treat his epilepsy, may reflect his desire for a successful outcome of the surgery. Placing the patient in a different environment or with different circumstances - say, locking him in a room with one of the facehuggers from the movie Alien - may lead to a reinterpretation of the same increased arousal as fear, instead of a general willingness to overcome the challenge that lays in front of him.

In any case, these results, coupled with the lack of emotional response to electrical charges delivered to control stimulation sites and sham stimulations, lends support to the theory that the midcingulate region plays some kind of role in motivation, and that stimluation to this region may have practical applications for disorders involving pathologically low amounts of motivation, such as major depression and senioritis; disorders which, I might add, I am fully qualified to treat with open-brain surgery and a homemade electrical stimulation kit consisting of copper wire and a couple of lemons. Just give me a call.


Link to paper (including video of interview with subject 1; scroll to bottom of page): http://www.sciencedirect.com/science/article/pii/S0896627313010301

Introduction to Computational Modeling: Hodgkin-Huxley Model

Computational modeling can be a tough nut to crack. I'm not just talking pistachio-shell dense; I'm talking walnut-shell dense. I'm talking a nut so tough that not even a nutcracker who's cracked nearly every damn nut on the planet could crack this mother, even if this nutcracker is so badass that he wears a leather jacket, and that leather jacket owns a leather jacket, and that leather jacket smokes meth.

That being said, the best approach to eat this whale is with small bites. That way, you can digest the blubber over a period of several weeks before you reach the waxy, delicious ambergris and eventually the meaty whale guts of computational modeling and feel your consciousness expand a thousandfold. And the best way to begin is with a single neuron.


The Hodgkin-Huxley Model, and the Hunt for the Giant Squid

Way back in the 1950s - all the way back in the twentieth century - a team of notorious outlaws named Hodgkin and Huxley became obsessed and tormented by fevered dreams and hallucinations of the Giant Squid Neuron. (The neurons of a giant squid are, compared to every other creature on the planet, giant. That is why it is called the giant squid. Pay attention.)

After a series of appeals to Holy Roman Emperor Charles V and Pope Stephen II, Hodgkin and Huxley finally secured a commission to hunt the elusive giant squid and sailed to the middle of the Pacific Ocean in a skiff made out of the bones and fingernails and flayed skins of their enemies. Finally spotting the vast abhorrence of the giant squid, Hodgkin and Huxley gave chase over the fiercest seas and most violent winds of the Pacific, and after a tense, exhausting three-day hunt, finally cornered the giant squid in the darkest netherregions of the Marianas Trench. The giant squid sued for mercy, citing precedents and torts of bygone eras, quoting Blackstone and Coke, Anaxamander and Thales. But Huxley, his eyes shining with the cold light of purest hate, smashed his fist through the forehead of the dread beast which erupted in a bloody Vesuvius of brains and bits of bone both sphenoidal and ethmoidal intermixed and Hodgkin screamed and vomited simultaneously. And there stood Huxley triumphant, withdrawing his hand oversized with coagulate gore and clutching the prized Giant Squid Neuron. Hodgkin looked at him.

"Huxley, m'boy, that was cold-blooded!" he ejaculated.
"Yea, oy'm one mean cat, ain't I, guv?" said Huxley.
"'Dis here Pope Stephen II wanted this bloke alive, you twit!"
"Oy, not m'fault, guv," said Huxley, his grim smile twisting into a wicked sneer. "Things got outta hand."


Scene II

Drunk with victory, Hodgkin and Huxley took the Giant Squid Neuron back to their magical laboratory in the Ice Cream Forest and started sticking a bunch of wires and electrodes in it. To their surprise, there was a difference in voltage between the inside of the neuron and the bath surrounding it, suggesting that there were different quantities of electrical charge on both sides of the cell membrane. In fact, at a resting state the neuron appeared to stabilize around -70mV, suggesting that there was more of a negative electrical charge inside the membrane than outside.

Keep in mind that when our friends Hodgkin and Huxley began their quest, nobody knew exactly how the membrane of a neuron worked. Scientists had observed action potentials and understood that electrical forces were involved somehow, but until the experiments of the 1940s and '50s the exact mechanisms were still unknown. However, through a series of carefully controlled studies, the experimenters were able to measure how both current and voltage interacted in their model neuron. It turned out that three ions - sodium (Na+), potassium (K+), and chlorine (Cl-) - appeared to play the most important role in depolarizing the cell membrane and generating an action potential. Different concentrations of the ions, along with the negative charge inside the membrane, led to different pressures exerted on each of the ions.

For example, K+ was found to be much more concentrated inside of the neuron than outside, leading to a concentration gradient exerting pressure for the K+ ions to exit the cell; at the same time, however, the attractive negative force inside the membrane exerting a countering electrostatic pressure, as positively charged potassium ions would be drawn toward the inside of the cell. Similar characteristics of the sodium and chlorine ions were observed as well, as shown in the following figure:

Ned the Neuron, filled with Neuron Goo. Note that the gradient and electrostatic pressures, expressed in microvolts (mV) have arbitrary signs; the point is to show that for an ion like chlorine, the pressures cancel out, while for an ion like potassium, there is slightly more pressure to exit the cell than enter it. Also, if you noticed that these values aren't 100% accurate, then congratu-frickin-lations, you're smarter than I am, but there is no way in HECK that I am redoing this in Microsoft Paint.

In addition to these passive forces, Hodgkin and Huxley also observed an active, energy-consuming force in maintaining the resting potential - a mechanism which exchanged potassium for sodium ions, by kicking out roughly three sodium ions for each potassium ion. Even with this pump though, there is still a whopping 120mV of pressure for sodium ions to enter. What prevents them from rushing in there and trashing the place?

Hodgkin and Huxley hypothesized that certain channels in the neuron membrane were selectively permeable, meaning that only specific ions could pass through them. Furthermore, channels could be either open or closed; for example, there may be sodium channels dotting the membrane, but at a resting potential they are usually closed. In addition, Hodgkin and Huxley thought that within these channels were gates that regulated whether the channel was open or closed, and that these gates could be in either permissive or non-permissive states. The probability of a gate being in either state was dependent on the voltage difference between the inside and the outside of the membrane.

Although this all may seem conceptually straightforward, keep in mind that Hodgkin and Huxley were among the first to combine all of these properties into one unified model - something which could account for the conductances, voltage, and current, as well as how all of this affected the gates within each ion channel - and they were basically doing it from scratch. Also keep in mind that these crazy mofos didn't have stuff like Matlab or R to help them out; they did this the old-fashioned way, by changing one thing at a time and measuring that shit by hand. Insane. (Also think about how, in the good old days, people like Carthaginians and Romans and Greeks would march across entire continents for months, years sometimes, just to slaughter each other. Continents! These days, my idea of a taxing cardiovascular workout is operating a stapler.) To show how they did this for quantifying the relationship between voltage and conductance in potassium, for example, they simply applied a bunch of different currents, saw how it changed over time, and attempted to fit a mathematical function to it, which happens to fit quite nicely when you include n-gates and a fourth-power polynomial.

After a series of painstaking experiments and measurements, Hodgkin and Huxley calculated values for the conductances and equilibrium voltages for different ions. Quite a feat, when you couple that with the fact that they hunted down and killed their very own Giant Squid and then ripped a neuron out of its brain. Incredible. That is the very definition of alpha male behavior, and it's something I want all of my readers to emulate.

Table 3 from Hodgkin & Huxley (1952) showing empirical values for voltages and conductances, as well as the capacitance of the membrane.

The same procedure was used for the n, m, and h gates, which were also found to be functions of the membrane voltage. Once these were calculated, then the conductances and voltage potential could be found for any resting potential and any amount of injected current.

H & H's formulas for the n, m, and h gates as a function of voltage.

So where does that leave us? Since Hodgkin and Huxley have already done most of the heavy lifting for us, all we need to do is take their constants and equations they've already derived, and put it into a script that we can then run through Matlab. At some point, just to get some additional exercise, we may also operate a stapler.

But stay focused here. Most of the formulas and constants can simply be transcribed from their papers into a Matlab script, but we also need to think about the final output that we want, and how we are going to plot it. Note that the original Hodgkin and Huxley paper uses a differential formula for voltage to tie together the capacitance and conductance of the membrance, e.g.:

We can use a method like Euler first-order approximation to plot the voltages, in which each time step is based off of the previous one which is added to a function multiplied by a time step; in the sample code below, the time step can be extremely small, thus giving a better approximation to the true shape of the voltage timecourse. (See the "calculate the derivatives" section below.)

The following code runs a simulation of the Hodgkin Huxley model over 100 milliseconds with 50mA of current, although you are encouraged to try your own and see what happens. The sample plots below show the results of a typical simulation; namely, that the voltage depolarizes after receiving a large enough current and briefly becomes positive before returning to its previous resting potential. The conductances of sodium and potassium show that the sodium channels are quickly opened and quickly closed, while the potassium channels take relatively longer to open and longer to close.The point of the script is to show how equations from papers can be transcribed into code and then run to simulate what neural activity should look like under certain conditions. This can then be expanded into more complex areas such as memory, cognition, and learning.

The actual neuron, of course, is nowhere to be seen; and thank God for that, else we would run out of Giant Squids before you could say Jack Robinson.


Resources
Book of GENESIS, Chapter 4
Original Hodgkin & Huxley paper


%===simulation time===
simulationTime = 100; %in milliseconds
deltaT=.01;
t=0:deltaT:simulationTime;


%===specify the external current I===
changeTimes = [0]; %in milliseconds
currentLevels = [50]; %Change this to see effect of different currents on voltage (Suggested values: 3, 20, 50, 1000)

%Set externally applied current across time
%Here, first 500 timesteps are at current of 50, next 1500 timesteps at
%current of zero (resets resting potential of neuron), and the rest of
%timesteps are at constant current
I(1:500) = currentLevels; I(501:2000) = 0; I(2001:numel(t)) = currentLevels;
%Comment out the above line and uncomment the line below for constant current, and observe effects on voltage timecourse
%I(1:numel(t)) = currentLevels;


%===constant parameters===%
%All of these can be found in Table 3
gbar_K=36; gbar_Na=120; g_L=.3;
E_K = -12; E_Na=115; E_L=10.6;
C=1;


%===set the initial states===%
V=0; %Baseline voltage
alpha_n = .01 * ( (10-V) / (exp((10-V)/10)-1) ); %Equation 12
beta_n = .125*exp(-V/80); %Equation 13
alpha_m = .1*( (25-V) / (exp((25-V)/10)-1) ); %Equation 20
beta_m = 4*exp(-V/18); %Equation 21
alpha_h = .07*exp(-V/20); %Equation 23
beta_h = 1/(exp((30-V)/10)+1); %Equation 24

n(1) = alpha_n/(alpha_n+beta_n); %Equation 9
m(1) = alpha_m/(alpha_m+beta_m); %Equation 18
h(1) = alpha_h/(alpha_h+beta_h); %Equation 18


for i=1:numel(t)-1 %Compute coefficients, currents, and derivates at each time step
   
    %---calculate the coefficients---%
    %Equations here are same as above, just calculating at each time step
    alpha_n(i) = .01 * ( (10-V(i)) / (exp((10-V(i))/10)-1) );
    beta_n(i) = .125*exp(-V(i)/80);
    alpha_m(i) = .1*( (25-V(i)) / (exp((25-V(i))/10)-1) );
    beta_m(i) = 4*exp(-V(i)/18);
    alpha_h(i) = .07*exp(-V(i)/20);
    beta_h(i) = 1/(exp((30-V(i))/10)+1);
   
   
    %---calculate the currents---%
    I_Na = (m(i)^3) * gbar_Na * h(i) * (V(i)-E_Na); %Equations 3 and 14
    I_K = (n(i)^4) * gbar_K * (V(i)-E_K); %Equations 4 and 6
    I_L = g_L *(V(i)-E_L); %Equation 5
    I_ion = I(i) - I_K - I_Na - I_L;
   
   
    %---calculate the derivatives using Euler first order approximation---%
    V(i+1) = V(i) + deltaT*I_ion/C;
    n(i+1) = n(i) + deltaT*(alpha_n(i) *(1-n(i)) - beta_n(i) * n(i)); %Equation 7
    m(i+1) = m(i) + deltaT*(alpha_m(i) *(1-m(i)) - beta_m(i) * m(i)); %Equation 15
    h(i+1) = h(i) + deltaT*(alpha_h(i) *(1-h(i)) - beta_h(i) * h(i)); %Equation 16

end


V = V-70; %Set resting potential to -70mv

%===plot Voltage===%
plot(t,V,'LineWidth',3)
hold on
legend({'voltage'})
ylabel('Voltage (mv)')
xlabel('time (ms)')
title('Voltage over Time in Simulated Neuron')


%===plot Conductance===%
figure
p1 = plot(t,gbar_K*n.^4,'LineWidth',2);
hold on
p2 = plot(t,gbar_Na*(m.^3).*h,'r','LineWidth',2);
legend([p1, p2], 'Conductance for Potassium', 'Conductance for Sodium')
ylabel('Conductance')
xlabel('time (ms)')
title('Conductance for Potassium and Sodium Ions in Simulated Neuron')

Comprehensive Computational Model of ACC: Expected Value of Control

Figure 1: Example of cognitive control failure

A new comprehensive computational model of dorsal anterior cingulate cortex function (dACC) was published in last week's issue of Neuron, sending shockwaves throughout the computational modeling community and sending computational modelers running to neuroscience magazinestands in droves. (That's right, I used the word droves - and you know I reserve that word only for special cases.)

The new model, published by Shenhav, Botvinick, and Cohen, attempts to unify existing models and empirical data of dACC function by modifying the traditional monitoring role usually ascribed to the dACC. In previous models of dACC function, such as error detection and conflict monitoring, the primary role of the dACC was that of a monitor involved in detecting errors, or monitoring for mutually exclusive responses and signaling the need to override prepotent but potentially wrong responses. The current model, on the other hand, suggests that the dACC monitors the expected value associated with certain responses, and weighs the potential cost of recruiting more cognitive control against the potential value (e.g., reward or other positive outcome) for implementing cognitive control.

This kind of tradeoff is best illustrated with a basic task like the Stroop task, where a color word - such as "green" - is presented in an incongruent ink, such as red. The instructions in this task are to respond to the color, and not the word; however, this is difficult since reading a word is an automatic process. Overriding this automatic tendency to respond to the word itself requires cognitive control, or strengthening task-relevant associations - in this case, focusing more on the color and not the word itself.

However, there is a drawback: using cognitive control requires effort, and effort isn't always pleasant. Therefore, it stands to reason that the positives for expending this mental effort should outweigh the negatives of using cognitive control. The following figure shows this as a series of meters with greater cognitive control going from left to right:

Figure 1B from Shenhav et al, 2013

As the meters for control signal intensity increase, so does the probability of choosing the correct option that will lead to positive feedback, as shown by the increasing thickness of the arrows from left to right. The role of the dACC, according to the model, is to make sure that the amount of cognitive control implemented is optimal: if someone always goes balls-to-the-wall with the amount of cognitive control they bring to the table, they will probably expend far more energy then would be necessary, even though they would have a much higher probability of being correct every time. (Study question: Do you know anybody like this?) Thus, the dACC attempts to reach a balance between the cognitive control needed and the value of the outcome, as shown in the middle column of the above figure.

This balance is referred to as the expected value of control (EVC): the difference between control costs and outcome values you can expect for a range of control signal intensities. The expected value can be plotted as a curve integrating both the costs and benefits of increased control, with a clear peak at the level of intensity that maximizes the difference between the expected payoff and control cost (Figure 2):

EVC curves (in blue) integrating costs and payoffs for control intensity. (Reproduced from Figure 4 from Shenhav et al, 2013)

That, in very broad strokes, is the essence of the EVC model. There are, of course, other aspects to it, including a role for the dACC in choosing the control identity which orients toward the appropriate behavior and response-outcome associations (for example, actually paying attention to the color of the stroop stimulus in the first place), which can be read about in further detail in the paper. Overall, the model seems to strike a good balance between complexity and conciseness, and the equations are relatively straightforward and should be easy to implement for anyone looking to run their own simulations.

So, the next time you see a supermodel in a bathtub full of Nutella inviting you to join her, be aware that there are several different, conflicting impulses being processed in your dorsal anterior cingulate. To wit, 1) How did this chick get in my bathtub? 2) How did she fill it up with Nutella? Do they sell that stuff wholesale at CostCo or something? and 3) What is the tradeoff between exerting enough control to just say no, given that eating that much chocolate hazelnut spread will cause me to be unable to move for the next three days, and giving in to temptation? It is a question that speaks directly to the human condition; between abjuring gluttony and the million ailments that follow on vice, and simply giving in, dragging that broad out of your bathtub and toweling the chocolate off her so you don't waste any of it, showing her the door, and then returning to the tub and plunging your insatiable maw into that chocolatey reservoir of bliss, that muddy fountain of pleasure, and inhaling pure ecstasy.