How to Fake Data and Get Tons of Money: Part 1

In what I hope will become a long-running serial, today we will discuss how you can prevaricate, dissemble, equivocate, and in general become as slippery as an eel slathered with axle grease, yet still maintain your mediocre, ill-deserved, but unblemished reputation, without feeling like a repulsive stain on the undergarments of the universe.

I am, of course, talking about making stuff up.

As the human imagination is one of the most wonderful and powerful aspects of our nature, there is no reason you should not exercise it to the best of your ability; and there is no greater opportunity to use this faculty than when the stakes are dire, the potential losses abysmally, wretchedly low, the potential gains dizzyingly, intoxicatingly high. (To get yourself in the right frame of mind, I recommend Dostoyevsky's novella The Gambler.) And I can think of no greater stakes than in reporting scientific data, when entire grants can turn on just one analysis, one result, one number. Every person, at one time or another, has been tempted to cheat and swindle their way to fortune; and as all are equally disposed to sin, all are equally guilty.

In order to earn your fortune, therefore, and to elicit the admiration, envy, and insensate jealousy of your colleagues, I humbly suggest using none other than the lowly correlation. Taught in every introductory statistics class, a correlation is simply a quantitative description of the association between two variables; it can range between -1 and +1; and the farther away from zero, the stronger the correlation, while the closer to zero, the weaker the correlation. However, the beauty of correlation is that one number - just one! - has the inordinate ability to make the correlation significant or not significant.Take, for example, the correlation between shoe size and IQ. Most would intuit that there is no relationship between the two, and that having a larger shoe size should neither be associated with a higher IQ or a lower IQ. However, if Bozo the Clown is included in your sample - a man with a gigantic shoe size, and who happens to also be a comedic genius - then your correlation could be spuriously driven upward by this one observation.

To illustrate just how easy this is, a recently created web applet provides you with fourteen randomly generated numbers, and allows the user to plot an additional point anywhere on the graph. As you will soon learn, it is simple to place the observation in a reasonable and semi-random location, and get the result that you want:

Non-significant correlation, leading to despair, despond, and death.

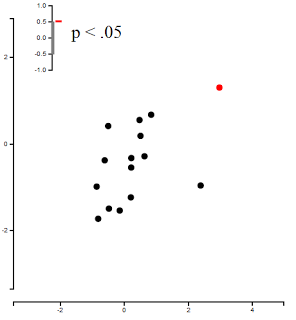Significant correlation, leading to elation, ebullience, and aphrodisia.

The beauty of this approach lies in its simplicity: We are only altering one number, after all, and this hardly approaches the enormity of scientific fraud perpetrated on far grander scales. It is easy, efficient, and fiendishly inconspicuous, and should anyone's suspicions be aroused, that one number can simply be dismissed as a clerical error, fat-finger typing, or simply chalked up to plain carelessness. In any case, it requires a minimum of effort, promises a maximum of return, and allows you to cover your tracks like the vulpine, versatile genius that you are.

And should your conscience, in your most private moments, ever raise objection to your spineless behavior, merely repeat this mantra to smother it: Others have done worse.

Super Useful Sampling Distributions Applet

Similar to the applets I used for my P211 research methods class, there is an online program which allows the user to specify a population distribution, and then build a sampling distribution of statistics such as mean, median, and variance. When I was first starting out I had a difficult time grasping what exactly a sampling distribution was, or what it meant, exactly; but tools like this are great for visualizing the process and building an intuition about what's really going on. The result is, I still don't understand it - like, at all - but I sure as hell feel more confident. And that's what is really important.

Bootstrapping

As I am covering bootstrapping and resampling in one of my lab sections right now, I felt I should share a delicious little applet that we have been using. (Doesn't that word just sound delicious? As though you could take a juicy bite into it. Try it!)

I admit that, before teaching this, I had little idea of what bootstrapping was. It seemed a recondite term only used by statistical nerds and computational modelers; and whenever it was mentioned in my presence, I merely nodded and hoped nobody else noticed my burning shame - while in my most private moments I would curse the name of bootstrapping, and shed tears of blood.

However, while I find that the concept of bootstrapping still surpasses all understanding, I now have a faint idea of what it does. And as it has rescued me from the abyss of ignorance and impotent fury, so shall this applet show you the way.

Bootstrapping is a resampling technique that can be used when there are few or no parametric assumptions  - such as a normal distribution of the population - or when the sample size is relatively small. (The size of your sample is to be neither a source of pride nor shame. If you have been endowed with a large sample, do not go waving it in the faces of others; likewise, should your sample be small and puny, do not hide it under a bushel.) Say that we have a sample of eight subjects, and we wish to generalize these results to a larger population. Resampling allows us to use any of those subjects in a new sample by randomly sampling with replacement; in other words we can sample one of our subjects more than once. If we assume that each original subject was randomly sampled from the population, then each subject can be used as a surrogate for another subject in the population - as if we had randomly sampled again.

After doing this resampling with replacement thousands or tens of thousands of times, we can then calculate the mean across all of those samples, plot them, and see whether 95% of the resampled means contains or excludes zero - in other words, whether our observed mean is statistically significant or not. (Here I realize that, as we are not calculating a critical value, the usual meaning of a p-value or 95% confidence interval is not entirely accurate; however, for the moment just try to sweep this minor annoyance under the rug. There, all better.)

The applet can be downloaded here. I have also made a brief tutorial about how to use the applet; if you ever happen to teach this in your own class, just tell the students that if the blue thing is in the gray thing, then your result fails to reach significance; likewise, if the blue thing is outside of the gray thing, then your result is significant, and should be celebrated with a continuous bacchanalia.