Just when FMRI researchers were feeling good and secure about the methods they were using, yet another paper has come out in the journal
Neuroimage about how everything you are doing is, to put it mildly, totally wrong.
The article, by Woo, Krishnan, and Wager, points out that one of the most popular correction methods for FMRI data - namely, cluster-correction, or cluster-extent thresholding - is routinely mishandled. This is not to say that you, a typical FMRI researcher, has no idea what he is doing. It is just that, when it comes to cluster-correction thresholding, you are about as competent as a bean burrito.
Cluster-correction is based on the assumption that in an FMRI dataset composed of several tens of thousands of voxels all abutting each other, there is likely to be some correlation in the observed signal between adjacent voxels. That is, one voxel immediately surrounded by several other voxels is not completely independent of its neighbors; the signal in each will be somewhat similar to the others, and this similarity is roughly related to how close the voxels are to each other. Smoothing, another common preprocessing practice, also introduces more spatial interpolations by averaging the signal over several voxels of a specified range, or kernel. Cluster-correction then uses an algorithm, such as Gaussian Random Field (GRF) Theory or Monte Carlo simulations, to determine what number of contiguous voxels at an individual, voxel-wise p-threshold (here in the paper referred to as a
primary p-thresholds) would be found due to chance alone; if a cluster of a certain size is exceedingly rare, then most researcher reject the null hypothesis and state that there is a significant effect in that cluster.
However, the authors point out that this can lead to erroneous interpretations about where, exactly, the significant effect is. All that you can say about a significant cluster is that the cluster itself is significant; cluster-correction makes no claims about which particular
voxels are significant. This can be a problem when clusters span multiple anatomical areas, such as a cluster in the insula spreading into the basal ganglia; it is not necessarily true that both the insula and basal ganglia are active, just that the cluster is. Large cluster sizes and lax primary p-thresholds, at the extremes, can lead to cluster sizes that are, relative to the rest of the brain, the size of a Goodyear Blimp.
 |
| Figure 1 from Woo et al (2014). A: Demonstration of how all of the different correction techniques, when plotted together, looks like a doughnut. Also, cluster-correction is the most popular technique. B and C: Clusters can span several areas, leading to erroneous interpretations about the spatial specificity of activation. |
Another issue is that large primary p-thresholds are correlated with larger cluster sizes passing correction. That is, only cluster sizes that are huge will be deemed significant. Obviously, this loss of spatial specificity can be a problem when attempting to study small areas, such as the periaqueductal gray, which is about the size of a strip of Stride gum, as shown in the following figure:
 |
| From left to right: Periaqueductal gray, Stride gum, Tom Cruise (all images shown to size) |
Lastly, the authors ran simulations to show that, even in a simulated brain with clearly demarcated "true signal" regions, liberal primary p-thresholds led to excessively high false discovery rates, a measurement of the number of false positives within a given dataset. (False discovery rate, or FDR, can be used as an alternative significance measurement, in which one is willing to tolerate a given percentage of false positives within a dataset - such as 5% or less - but is agnostic about
which voxels are false positives.) This also led to a high amount of clusters smearing across the true signal regions and into areas which did not contain signal:
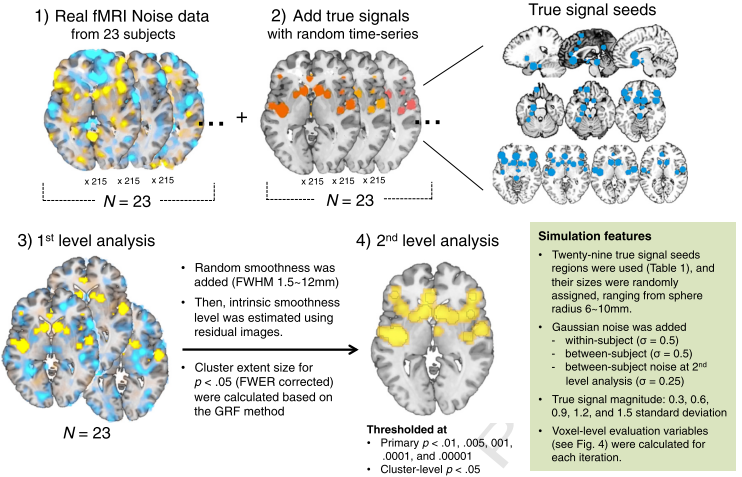 |
| Figure 3 from Woo et al, 2014 |
Problems like these can be ameliorated by choosing more stringent primary p-thresholds, such as a voxelwise p less than 0.001, and in cases where power is sufficiently high or in cases where you might suspect that the intrinsic smoothness of your dataset is highly irregular, you may want to eschew cluster correction altogether and use a voxel-wise correction method such as family-wise error (FWE) or FDR. If you do use cluster correction, however, and you still get blobs that look like messy fingerpaintings, it can help the reader to clearly demarcate the boundaries of the clusters with different colors, thereby helping visualize the size and extent of the clusters, and fulfilling some of your artistic needs.
Now go eat your bean burrito.




