For most people, doing first-level analyses in SPM is tedious in the extreme; for other people, these analyses are manageable through command line scripting in Matlab. And there are still other people who don't even think about first-level analyses or SPM or Matlab or any of that. This last class of people are your college classmates who majored in something else, like economics, and are living significantly less stressful lives than you, making scads of money, and regularly eating out at restaurants where they serve shrimp the size of Mike Tyson's forearm.
Assuming that you belong to the first category, however, first-level analyses are invariably a crashing bore; and, worse, completely impractical for something like beta-series analysis, where a separate regressor is needed for individual events.
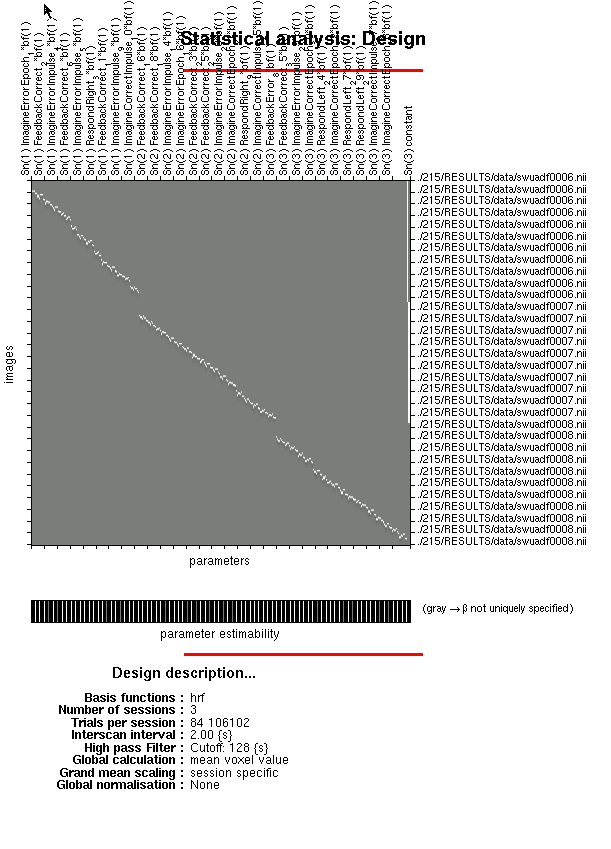
The following script will do all of that for you, although it makes many assumptions about your timing files and where everything is stored. First, your directory needs to be set up with a root directory containing all of the subjects, as well as a separate timing directory containing your onsets files; and second, that the timing files are written in a four-column format of runs, regressors, onsets (in seconds), and duration. Once you have all of that, though, all it takes is simply modifications of the script to run your analysis.
As always, let me know if this actually helps, or whether there are sections of code that can be cleaned up. I will be making a modification tomorrow allowing for beta series analysis by converting all of the timing events into individual regressors, which should help things out.
Link to script:
http://mypage.iu.edu/~ajahn/docs/Run_SPM_FirstLevel.m
% INPUT:
% rootDir - Path to where subjects are located
% subjects - Vector containing list of subjects (can concatenate with brackets)
% spmDir - Path to folder where you want to move the multiple conditions .mat files and where to the output SPM file (directory is created if it doesn't
% exist)
% timingDir - Path to timing directory, relative to rootDir
% timingSuffix - Suffix appended to timing files
% matPrefix - Will be prefixed to output .mat files.
% dataDir - Directory storing functional runs.
%
% OUTPUT:
% One multiple condition .mat file per run. Also specifies the GLM and runs
% beta estimation.
%
%
% Note that this script assumes that your timing files are organized
% with columns in the following order: Run, ConditionName, Onset (in
% seconds), Duration (in seconds)
%
% Ideally, this timing file should be written out from your
% presentation software, e.g., E-Prime
%
% Also note how the directory tree is structured in the following example. You may have to
% change this script to reflect your directory structure.
%
% Assume that:
% rootdir = '/server/studyDirectory/'
% spmDir = '/modelOutput/'
% timingDir = '/timings/onsets/'
% subjects = [101]
% timingSuffix = '_timing.txt'
% 1) Sample path to SPM directory:
% '/server/studyDirectory/101/modelOutput/'
% 2) Sample path to timing file in the timing directory:
% '/server/studyDirectory/timings/onsets/101_timing.txt'
%
% Andrew Jahn, Indiana University, June 2014
% andysbrainblog.blogspot.com
clear all
%%%----Things you will want to change for your study----%%%
rootDir = '/data/hammer/space5/ImagineMove/fmri/';
subjects = [214 215];
spmDir = '/RESULTS/testMultis/';
timingDir = 'fMRI_behav/matlab_input/';
timingSuffix = '_spm_mixed.txt';
matPrefix = 'testMulti';
dataDir = '/RESULTS/data/';
%Change these parameters to reflect study-specific information about number
%of scans and discarded acquisitions (disacqs) per run
funcs = {'swuadf0006.nii', 'swuadf0007.nii', 'swuadf0008.nii'}; %You can add more functional runs; just remember to separate them with a comma
numScans = [240 240 240]; %This if the number of scans that you acquire per run
disacqs = 2; %This is the number of scans you later discard during preprocessing
numScans = numScans-disacqs;
TR = 2; %Repetition time, in seconds
%Estimating the GLM can take some time, particularly if you have a lot of betas. If you just want to specify your
%design matrix so that you can assess it for singularities, turn this to 0.
%If you wish to do it later, estimating the GLM through the GUI is very
%quick.
ESTIMATE_GLM = 1;
%%%-----------------------------------------------------%%%
%For each subject, create timing files and jobs structure
for subject = subjects
%See whether output directory exists; if it doesn't, create it
outputDir = [rootDir num2str(subject) spmDir];
if ~exist(outputDir)
mkdir(outputDir)
end
%---Navigate to timing directory and create .mat files for each run---%
cd([rootDir timingDir]);
fid = fopen([num2str(subject) timingSuffix], 'rt');
T = textscan(fid, '%f %s %f %f', 'HeaderLines', 1); %Columns should be 1)Run, 2)Regressor Name, 3) Onset Time (in seconds, relative to start of each run), and 4)Duration, in seconds
fclose(fid);
clear runs nameList names onsets durations sizeOnsets %Remove these variables if left over from previous analysis
runs = unique(T{1});
%Begin creating jobs structure
jobs{1}.stats{1}.fmri_spec.dir = cellstr(outputDir);
jobs{1}.stats{1}.fmri_spec.timing.units = 'secs';
jobs{1}.stats{1}.fmri_spec.timing.RT = TR;
jobs{1}.stats{1}.fmri_spec.timing.fmri_t = 16;
jobs{1}.stats{1}.fmri_spec.timing.fmri_t0 = 1;
%Create multiple conditions .mat file for each run
for runIdx = 1:size(runs, 1)
nameList = unique(T{2});
names = nameList';
onsets = cell(1, size(nameList,1));
durations = cell(1, size(nameList,1));
sizeOnsets = size(T{3}, 1);
for nameIdx = 1:size(nameList,1)
for idx = 1:sizeOnsets
if isequal(T{2}{idx}, nameList{nameIdx}) && T{1}(idx) == runIdx
onsets{nameIdx} = double([onsets{nameIdx} T{3}(idx)]);
durations{nameIdx} = double([durations{nameIdx} T{4}(idx)]);
end
end
onsets{nameIdx} = (onsets{nameIdx} - (TR*disacqs)); %Adjust timing for discarded acquisitions
end
save ([matPrefix '_' num2str(subject) '_' num2str(runIdx)], 'names', 'onsets', 'durations')
%Grab frames for each run using spm_select, and fill in session
%information within jobs structure
files = spm_select('ExtFPList', [rootDir num2str(subject) dataDir], ['^' funcs{runIdx}], 1:numScans);
jobs{1}.stats{1}.fmri_spec.sess(runIdx).scans = cellstr(files);
jobs{1}.stats{1}.fmri_spec.sess(runIdx).cond = struct('name', {}, 'onset', {}, 'duration', {}, 'tmod', {}, 'pmod', {});
jobs{1}.stats{1}.fmri_spec.sess(runIdx).multi = cellstr([outputDir matPrefix '_' num2str(subject) '_' num2str(runIdx) '.mat']);
jobs{1}.stats{1}.fmri_spec.sess(runIdx).regress = struct('name', {}, 'val', {});
jobs{1}.stats{1}.fmri_spec.sess(runIdx).multi_reg = {''};
jobs{1}.stats{1}.fmri_spec.sess(runIdx).hpf = 128;
end
movefile([matPrefix '_' num2str(subject) '_*.mat'], outputDir)
%Fill in the rest of the jobs fields
jobs{1}.stats{1}.fmri_spec.fact = struct('name', {}, 'levels', {});
jobs{1}.stats{1}.fmri_spec.bases.hrf = struct('derivs', [0 0]);
jobs{1}.stats{1}.fmri_spec.volt = 1;
jobs{1}.stats{1}.fmri_spec.global = 'None';
jobs{1}.stats{1}.fmri_spec.mask = {''};
jobs{1}.stats{1}.fmri_spec.cvi = 'AR(1)';
%Navigate to output directory, specify and estimate GLM
cd(outputDir);
spm_jobman('run', jobs)
if ESTIMATE_GLM == 1
load SPM;
spm_spm(SPM);
end
end
%Uncomment the following line if you want to debug
%keyboard