What Smoothing Is
Smoothing, the process of introducing spatial correlation into your data by averaging across nearby data points (in fMRI datasets, nearby voxels) is an essential step in any preprocessing stream. Traditionally, smoothing applies a Gaussian filter to average signal over nearby voxels in order to summate any signal that is present, while attenuating and cancelling out noise. This step also has the advantage of spreading signal over brain areas that have some variation across subjects, leading to increased signal-to-noise ratio over larger cortical areas at the loss of some spatial specificity. Lastly, smoothing mitigates the fiendish multiple comparisons problem, since voxels are not truly independent in the first place (neither are timepoints, but more on this at a later time).
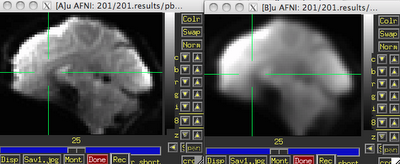 |
| Before (left) and after (right) smoothing. Note that there is much more spatial detail in the image before smoothing is applied. |
Usually this smoothing step is taken care of by your fMRI software analysis package's built-in smoothing program, but something I learned back at the AFNI bootcamp is that images coming off the scanner are already smoothed, i.e., there is already some inherent spatial correlation in the data. This makes sense, given that functional imaging datasets are acquired at relatively low resolution, and that voxels with a given intensity will most likely be immediately surrounded by other voxels with similar intensities. In the above image on the left which has not been smoothed, voxels that are brighter tend to cluster together, while voxels that are darker tend to cluster together. This spatial correlation will be increased with any additional step requiring spatial interpolation, including coregistration (aligning all volumes in a run to a reference volume), normalization (warping an image to a template space), and smoothing.
Smoothing Programs in AFNI: 3dmerge and 3dBlurToFWHM
In the good old days, the staple program for blurring in AFNI was 3dmerge with the -blur option. Since 2006, there has been a new program, 3dBlurToFWHM, which estimates the smoothness of the dataset, and attempts to smooth only to specified blur amounts in the x, y, and z directions. (Another thing I didn't recognize, in my callow youth, was that there can indeed be different smoothness amounts along the axes of your dataset, which in turn should be accounted for by your smoothing algorithm.) 3dmerge will add on the specified smoothness to whatever smoothness is already present in the data, so the actual smoothness of the data is not what is specified on the command line with 3dmerge. For example, if 3dmerge with a 6mm Full-Width at Half-Maximum (FWHM) is applied to a dataset that already has smoothness of about 3mm in the x, y, and z directions, the resulting smoothness will be about 8-9mm. (This example, similar to many simulations carried out in the lab, is not a purely linear addition, but is relatively close.)
3dBlurToFWHM, on the other hand, will begin with estimating the smoothness of your dataset, and then iteratively blur (i.e., smooth) the data until it reaches the desired level of smoothness in the x, y, and z directions. These can be specified separately, but often it is more useful to use the same value for all three. For example, the following command will blur a dataset until it reaches approximately 6mm of smoothness in each direction:
3dBlurToFWHM -FWHM 6 -automask -prefix outputDataset
Applying this to a dataset that has been coregistered and normalized will produce output that looks like this:
Note that the first set of numbers highlighted in red are the estimates produced by 3dBlurToFWHM, and the last set of numbers of red are estimates from a separate program, 3dFWHMx. The reason for the discrepancy is that 3dBlurToFWHM uses a slightly faster and less accurate estimator when blurring; however, the two sets of numbers are functionally equivalent. In any case, the resulting blur estimates are very close to the specified FWHM kernel, typically within 10% or less.
What Mask to Use?
Often using a mask generated after the coregistration step (i.e., the 3dvolreg command) is sufficient, such as full_mask+tlrc or mask_epi_extents+tlrc. The -automask option can also be used, which usually works just as well. The only considerations to take into account are that masking out non-brain voxels will limit your field of view; some experienced users advise not masking until after performing statistical tests, as artifacts or consistent signal outside of the brain can point to hardware problems or issues with your experimental design.What to Use for the -blurmaster Option?
According to the AFNI help for 3dBlurToFWHM, the -blurmaster option can be used to control the smoothing process, which can lead to slightly better smoothing results. As the FWHM is supposed to represent the underlying spatial structure of the noise, and not the spatial structure of the brain's anatomy, using a dataset of residuals is often a good choice here; for example, the output of -errts in 3dDeconvolve. However, this requires running 3dDeconvolve first, and then using the errts dataset in the blurmaster option all over again. This is usually more trouble than it's worth, as I haven't found significant differences between having a blurmaster dataset and not having one.
Estimating Smoothness with 3dFWHMx
After blurring your data, 3dFWHMx can be used to estimate the smoothness of a given dataset. Useful options are -geom, to estimate the geometric mean of the smoothness, and -detrend, which accounts for outlier voxels. For example,3dFWHMx -geom -detrend -input inputDataset
What about this 3dBlurInMask Thing?
3dBlurInMask does much the same thing as 3dBlurToFWHM, except that you can use multiple masks if you desire. This procedure may also be useful if you plan to only blur within, say, the gray matter of a dataset, although this can also lead to problems such as biasing signal in certain locations after the grey matter masks have all been warped to a template space, as there is far greater variability in smoothing across masks than there is applying a smoothing kernel to the same averaged mask that incorporates all of the brain voxels across all subjects.How to Estimate Smoothness in SPM
SPM comes with it's own smoothness estimation program, spm_est_smoothness. It requires a residuals dataset and a mask for which voxels to analyze. For example,[fwhm, res] = spm_est_smoothness('ResMS.hdr', 'mask.hdr')
Will return the estimated FWHM in the x, y, and z directions, as well as a structure containing information about the resels of the dataset.
Why it Matters
I tuned into this problem a couple months ago when one of my colleagues got nailed by a reviewer for potentially not estimating the smoothness in his dataset appropriately. Evidently, he had used the smoothing kernel specified in his preprocessing stream when calculating cluster correction thresholds, when in fact the actual smoothness of the data was higher than that. It turned out to be a non-significant difference, and his results held in either case. However, to be on the safe side, it always helps to report estimating your smoothness with an appropriate tool. If your results do significantly change as a result of your smoothness estimation approach, then your result may not have been as robust to begin with, and may require some more tweaking.(By tweaking, of course, I mean screwing around with your data until you get the result that you want.)

