Andy's Brain Blog

As part of a new course in neuroimaging methods at Haskins Laboratories, I've begun updating videos on topics such as functional connectivity, context-dependent correlations, and how to accept bribes as a reviewer. The first topic we've covered is resting-state functional connectivity, a sophisticated-sounding name designed to make the subject think he is doing something of immense scientific importance by lying still and doing nothing, when in reality it's to distract him while we find out how to hell to hook up the experimental laptop.

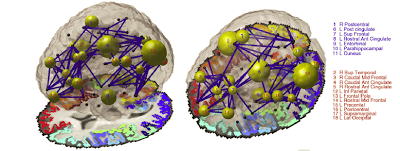
Aside from its usefulness as a stall tactic, resting-state connectivity can also reveal resting-state networks, or correlations between the signal of distant regions of the brain. This provides clues to how structural connectivity - i.e., white matter connections - interact with the BOLD signal, as well as whether differences in resting-state connectivity is a marker for mental disorders such as Alzheimer's or schizophrenia.

The following video takes you step-by-step through functional connectivity analysis, using an online dataset from openfmri.org. One major change from my previous tutorials is condensing all the information into one long video, and providing time markers for each segment in the "Show More" box. This way the viewer can jump around to the information that they need, without having to keep track of several different videos detailing different steps. I hope it's an improvement, and I would like to get feedback.

I've also posted the lecture on resting-state analysis given at Haskins Laboratories on November 3rd. You won't learn much new here that isn't in the video above, but it does have more information. For most of the lecture you can only see the top of my head bobbing around, but that's OK. Eyes on the slides, not the hair.

Exercises:

Set the errts dataset as the underlay, and select "Graph". From the "Opt" menu, select "Write Center." Rename the output 1D file, and use 1dplot to see the timecourse. This can be used as a seed for another connectivity analysis.
Other resting state networks include the somatosensory network, the visual network, and the language network. Research one of these networks, determine where the hubs are, and run a resting state analysis on a seed placed in that hub.
Run correlations for a group of subjects, convert to z-scores, and do a second-level t-test using uber_ttest.py.
Modify the afni_proc.py script to apply 3dRSFC to your data (see Example 10b in afni_proc.py -help)

The next time you look at your dwindling scanning budget and realize you need to start coming in at 9:00pm on Fridays to pay a reduced scanning rate, just remember that there are other researchers out there who scan hundreds of subjects for a single study. (This isn't supposed to make you feel better; it's just a fact.)

A recent connectivity analysis by Dennis and colleagues recruited four hundred and thirty-nine subjects for a cross-sectional study to determine changes in connectivity from the ages of twelve to thirty. Overall, older participants showed decreasing long-range connectivity between regions, increased modularity (a measure of subdivision within regions), and hemispheric differences in global efficiency, consistent with developmental theories that short-range connections are pruned during adolescence while long-range connections are strengthened.

However, the observed hemispheric differences in global efficiency contrasted with previous findings:

Our results are contrary to those of Iturria-Medina et al. (2011), who found greater global efficiency in the right hemisphere, but these were from a relatively small sample of 11 subjects, and our sample is over 40 times larger. [Emphasis added.]

Boom. Over forty times larger, son. Sit the hell down. "But forty times eleven is four hundred forty." Yeah, well, the jury's still out on mathematics. "But we ran a well-controlled study!" WHAT PART OF FORTY TIMES LARGER DON'T YOU UNDERSTAND?!

Proof that size equals power can be found here.